第82页 - 通城学典课时作业本九年级数学苏科版江苏专用

C

D

$\frac {\sqrt{3}}{2}$

$\frac {1}{2}$

$ 解：原式=2\sqrt{3}-|2×\frac {\sqrt{3}}{2}-2×1|-6×(\frac {\sqrt{2}}{2})²+\frac {25}{9}$

$ =2\sqrt{3}-2+\sqrt{3}-3+\frac {25}{9}$

$ =3\sqrt{3}-\frac {20}{9}$

$解：过点C作CD⊥AB于点D$

$∵∠A=30°，AC=\sqrt {6}，cosA=cos{30}°=\frac {AD}{AC}=\frac {\sqrt {3}}2$

$∴AD=\frac {3\sqrt {2}}2$

$∵sinA=sin{30}°=\frac {CD}{AC}=\frac 1 2$

$∴CD=\frac {\sqrt {6}}2$

$∵tanB=tan{45}°=\frac {CD}{BD}=1$

$∴BD=\frac {\sqrt {6}}2$

$∴AB=AD+BD=\frac {3\sqrt {2}+\sqrt {6}}2$

$在Rt△BCD中，由勾股定理，得$

$BC=\sqrt {{CD}^2+{BD}^2}=\sqrt {3}$

B

$解：原式=2+\frac {\sqrt {3}}3×\frac {\sqrt {3}}2$

$=2+\frac 1 2$

$=\frac 5 2$

$故答案为：C$

$解：∵四边形ABCD是矩形$

$∴AO=BO=CO=DO$

$∵∠AOB=60°$

$∴△AOB是等边三角形$

$∴AO=AB$

$∴AC=2AB$

$∴BC=\sqrt {3}AB$

$∴\frac {AB}{BC}=\frac {AB}{\sqrt {3}AB}=\frac {\sqrt {3}}3$

$故答案为：D$

解: ∵三角形的内角和为180°，∠A、∠B、∠C的度数之比为1:2:3，

设∠A=x, 则∠B=2x, ∠C=3x,

则有:x+2x+3x=180°, 解得:x=30°,

∴∠B=60°，

∴sinB=$\frac{\sqrt{3}}{2}$.

故答案为: $\frac {\sqrt 3}{2}$

$解：连接MF，MO，延长MO交EF于H，如图，$
$\because 直线MN与\odot O相切于点M，$
$\therefore MH\bot MN，$
$\because EF$∥$MN，$
$\therefore MH\bot EF，$
$\therefore EH=HF，即MH垂直平分EF，$
$\therefore ME=MF，$
$\because EM=EF，$
$\therefore EM=EF=MF，$
$\therefore \triangle MEF为等边三角形，$
$\therefore \angle MEF=60^{\circ}，$
$\therefore \cos E=\cos 60^{\circ}=\frac{1}{2}，$
$故答案为：\frac{1}{2}.$

$解：原式=2\sqrt{3}-|2×\frac {\sqrt{3}}{2}-2×1|-6×(\frac {\sqrt{2}}{2})²+\frac {25}{9}$

$=2\sqrt{3}-2+\sqrt{3}-3+\frac {25}{9}$

$=3\sqrt{3}-\frac {20}{9}$

$解：过点C作CD⊥AB于点D$

$∵∠A=30°，AC=\sqrt {6}，cosA=cos30°=\frac {AD}{AC}=\frac {\sqrt {3}}2$

$∴AD=\frac {3\sqrt {2}}2$

$∵sinA=sin30°=\frac {CD}{AC}=\frac 1 2$

$∴CD=\frac{\sqrt {6}}2$

$∵tanB=tan45°=\frac {CD}{BD}=1$

$∴BD=\frac {\sqrt {6}}2$

$∴AB=AD+BD=\frac {3\sqrt {2}+\sqrt {6}}2$

$在Rt△BCD中，由勾股定理，得$

$BC=\sqrt {{CD}^{2}+{BD}^{2}}=\sqrt {3}$

解：法一、如图，

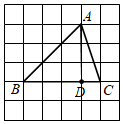
$在Rt\triangle ABD中，\angle ADB=90^{\circ}，AD=BD=3，$
$\therefore AB=\sqrt{A{D}^{2}+B{D}^{2}}=\sqrt{{3}^{2}+{3}^{2}}=3\sqrt{2}，$
$\therefore \cos \angle ABC=\frac{BD}{AB}=\frac{3}{3\sqrt{2}}=\frac{\sqrt{2}}{2}.$
$故选：B.$
$法二、在Rt\triangle ABD中，\angle ADB=90^{\circ}，AD=BD=3，$
$\therefore \angle ABD=\angle BAD=45^{\circ}，$
$\therefore \cos \angle ABC=\cos 45^{\circ}=\frac{\sqrt{2}}{2}.$
$故选：B.$