电子课本网 › 第25页

第25页

信息发布者：

证明：$∵∠BHC =∠FHD，$$∠GFH +∠BHC=180°$

$∴∠GFH+∠FHD=180°$

$∴FG//BD，$

$∴∠1=∠ABD$

$∵BD$平分$∠ABC$

$∴∠2=∠ABD，$

$∴∠1=∠2$

解：$(1)∵BE$平分$∠ABC，$

$∴∠ABC=2∠ABE，$

$∵∠ABC=2∠E，$

$∴∠ABE=∠E，$

$∴AB∥EF.$

$(2)AF$与$BE$的位置关系是垂直，理由如下：

$∵∠ADE=∠BCD.$

$∴AD∥BC，$

$∴∠DAB+∠CBA=180°，$

$∵BE$平分$∠ABC，$$AF_{平分}∠BAD，$

$∴∠ABC=2∠ABE，$$∠BAD=2∠BAF，$

$∴2∠ABE+2∠BAF=180°，$

$∴∠ABE+∠BAF=90°，$

$∴∠AOB=90°，$

$∴AF⊥BE.$

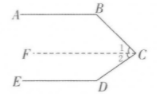
解$： (1) $如图，过点$C$作$CF // AB$

则$∠l+∠B=180° ($两直线平行，同旁内角互补)

$∴∠1=180°-∠B=180-135°=45°$

$∵CF// AB，$$AB// DE$

$∴CF// DE ($如果两条直线都与第三条直线平行，

那么这两条直线也互相平行)

同理，可得$∠2=180°-∠D=180°-145=35°$

$∴∠BCD=∠1+∠2=45°+35°=80°$

$(2)∠B+ ∠BCD+∠D=360°$

理由:如图，由$(1)$知，$CF//AB，$$CF// DE $

$∴∠B+∠1=180°，$$∠D+∠2=180° ($两直线平行，同旁内角互补)

$∴∠B+∠1+∠2+∠D=360°$

即$∠B+∠BCD+∠D=360°$

$(3)∠B+∠C+∠D+∠E=540°$

上一页下一页