解:$(1)$如图$1,$过点$P_{作}PQ∥AB,$
$∵AB∥CD,$
$∴PQ∥CD,$
$∵∠AEP=130°,$$∠PFD=80°,$
$∴∠QPF=80°,$$∠QPE=50°,$
$∴∠EPF=∠QPF-∠QPE=80°-50°=30°.$
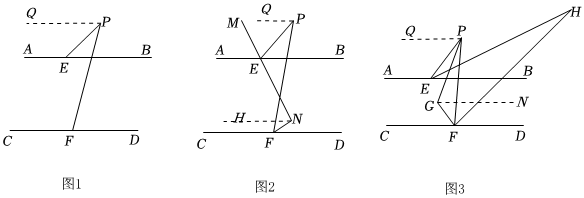
$(2)$如图$2,$过点$P{作}PQ∥AB,$过点$N$作$NH∥CD,$
$∵AB∥CD,$
$∴PQ∥CD∥AB∥NH,$
$∵EM$平分$∠AEP,$$FN$平分$∠PFD,$
设$∠AEM=∠MEP=α,$$∠PEN=∠NFD=β,$
则$∠PEN+∠EPF=(180°-2α+α)+[2β-(180°-2α)]=α+2β,$
$∵∠PFN+∠ENF=β+(α+β)=α+2β,$
$∴∠PEN+∠EPF=∠PFN+∠ENF.$
$(3)$如图$3,$过点$P{作}PQ∥AB,$过点$G{作}GN∥CD,$
$∵AB∥CD,$
$∴PQ∥CD∥AB∥NG,$
$∵EH$平分$∠PEB,$$FH$平分$∠PFD,$$FG{平分}∠PFC,$
设$∠PEH=∠HEB=α,$$∠PFH=∠HFD=β,$$∠EPG=∠GPF=x,$
$∠PFG=∠GFC=y,$
则$2β+2y=180°,$
$∵2β=2x+2α,$
$∴2x+2y+2α=180°,$
$∴x+y=90°-α,$$∠PGF=∠PGN+∠NGF=2α+x+y=2α+90°-α=90°+α,$
当$PE∥FH$时,$∠EHF=α,$
$∴∠PGF-∠EHF=90°.$