解:$(2)$在$PC$上截取$PD=AP,$连接$AD,$如图$1:$
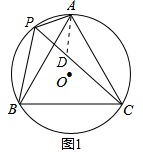
∵∠APC=60°,
$∴△APD$是等边三角形,
$∴AD=AP=PD,$$∠ADP=60°,$$∠ADC=120°.$
$∵∠APB=∠APC+∠BPC=120°,$
$∴∠ADC=∠APB.$
在$△APB$和$△ADC$中,$∠APB=∠ADC,$$∠ABP=∠ACD,$$AP=AD,$
$∴△APB≌△ADC,$
$∴BP=CD.$
又$∵PD=AP,$
$∴PC=PA+PB.$
$(3)$当点$P$为$\widehat{AB}$的中点时,四边形$APBC$的面积最大.
理由如下:如图$2,$过点$P$作$PE⊥AB,$垂足为$E,$过点$C$作$CF⊥AB,$垂足为$F.$
$∵S_{△APB}=\frac {1}{2}AB·PE,$$S_{△ABC}=\frac {1}{2}AB·CF,$
$∴S_{四边形APBC}=\frac {1}{2}AB·(PE+CF).$
当点$P$为$\widehat{AB}$的中点时,$PE+CF=PC,$$PC$为$⊙O$的直径,
∴此时四边形$APBC$的面积最大.
$∵⊙O$的半径为$1,$
∴其内接正三角形的边长$AB=\sqrt{3},$
$∴S_{四边形APBC}=\frac {1}{2}×2×\sqrt{3}=\sqrt{3}.$