解:$(1)$直线$AC$与$⊙O$相切,理由如下:
$∵∠ABC=45°,$$AB=AC,$
$∴∠ABC=∠C=45°,$
$∴∠BAC=180°-2×45°=90°,$
$∴BA⊥AC,$
$∵AB$是$⊙O$的直径,
∴直线$AC$与$⊙O$相切.
$(2)$连接$OD,$$AD,$
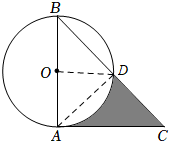
$∵AB$是$⊙O$的直径,
$∴∠ADB=90°,$
$∵∠ABD=45°,$
$∴△ABD$是等腰直角三角形,$∠AOD=90°,$
$∵AO=OB,$$AB=4,$
$∴S_{△ABD}=\frac {1}{2}•AB•OD=\frac {1}{2}×4×2=4,$
∴图中阴影部分的面积$=S_{△ABC}-S_{△BOD}-S_{扇形OAD}$
$=\frac {1}{2}×4×4-\frac {1}{2}×4-\frac {90π×2^2}{360}$
$=8-2-π$
$=6-π.$