第8页 - 通城学典课时作业本八年级数学人教版南通专版

证明：$(1)∵AD$平分$∠BAC，$$DE⊥AB，$$∠C=90°，$

$∴DC=DE，$

在$Rt△DCF $和$Rt△DEB$中，

$\{\begin{array}{l}{DC=DE}\\{DF=DB}\end{array}，$

$∴Rt△DCF≌Rt△DEB，$

$∴CF=EB.$

$(2)AF+BE=AE.$

$∵Rt△DCF≌Rt△DEB，$

$∴AC=AE，$

$∴AF+FC=AE，$

即$AF+BE=AE.$

解：$(1)$如图，$OP$即为$∠AOB$的角平分线.

在$OA$和$OB$上截取$OE=OF，$在$OP$上任取一点$C，$连接$CE，$$CF，$

则$△COE≌△COF.$

$(2)EF=DF.$

如图②，在$AC$上截取$AG=AE，$连接$FG.$

$∵AD$是$∠BAC$的平分线，

$∴∠1=∠2.$

在$△AEF $与$△AGF $中，

$\begin{cases}{AG=AE，}\\{∠1=∠2，}\\{AF=AF，}\end{cases}$

$∴△AEF≌△AGF，$

$∴∠AFE=∠AFG，$$FE=FG.$

$∵∠B=60°，$$AD，$$CE$分别是$∠BAC，$$∠BCA$的平分线，

$∴2∠2+2∠3+∠B=180°，$

$∴∠2+∠3=60°.$

又$∵∠AFE$为$△AFC$的外角，

$∴∠AFE=∠CFD=∠AFG=∠2+∠3=60°，$

$∴∠CFG=60°，$即$∠GFC=∠DFC.$

在$△CFG $与$△CFD$中，

$\begin{cases}{∠GFC=∠DFC，}\\{FC=FC，}\\{∠3=∠4，}\end{cases}$

$∴△CFG≌△CFD，$

$∴FG=FD，$

$∴FE=FD.$

55°

解$：(2)$如图$1，$过$A$作$AD⊥x$轴，$CE⊥x$轴，垂足分别为$D、$$E，$

$∵AD⊥x$轴，$CE⊥x$轴，

$∴∠ADB=∠BEC=90°，$

$∴∠DAB+∠ABD=90°，$

$∵AB⊥BC，$

$∴∠EBC+∠ABD=90°，$

$∴∠DAB=∠EBC，$

在$△ADB$与$△BEC$中，

$\begin{cases}{∠ADB=∠BEC}\\{∠DAB=∠EBC}\\{AB=BC}\end{cases}$

$∴△ADB≌△BEC(\mathrm {AAS})，$

$∴BD=CE，$

$∵A(3，$$3)，$$C(1，$$-1)，$

$∴OD=3，$$CE=1，$

$∴OB=OD+BD=OD+CE=3+1=4，$

$∴B(4，$$0).$

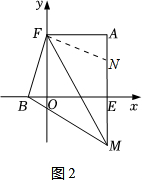
$(3)$解：如图$2，$在$AM$上截取$AN=OB，$连接$FN，$

$∵A(3，$$3)，$

$∴OF=AF=3，$

在$△BOF $与$△NAF $中，

$AN=OB$

$∠A=∠BOF$

$OF=AF$

$∴△BOF≌△NAF(\mathrm {SAS})，$

$∴∠BFO=∠NFA，$$BF=NF，$

$∵∠BFM=∠BFO+∠OFM=45°，$

$∴∠NFA+∠OFM=45°，$

$∵∠OFA=90°，$

$∴∠NFM=∠OFA-(∠NFA+∠OFM)=90°-45°=45°，$

$∴∠BFM=∠NFM，$

在$△BFM$与$△NFM$中，

$\begin{cases}{BF=AN}\\{∠BFM=∠NFM}\\{FM=FM}\end{cases}$

$∴△BFM≌△NFM(\mathrm {SAS})，$

$∴BM=NM，$

$∵BM=5，$$B(-1，$$0)，$

$∴MN=5，$$BO=AN=1，$

$∴EM=MN+AN-AE=5+1-3=3.$