$解:(2)① 由(1)知:抛物线的对称轴为直线x=2,顶点的坐标为\left(2,4\right)。$
$设点P的坐标为\left(2,m\right)\left(其中0\leqslant m\leqslant 4\right),$
$则P{C}^{2}={2}^{2}+(m-3{)}^{2},P{Q}^{2}={m}^{2}+(n-2{)}^{2},C{Q}^{2}={3}^{2}+{n}^{2}$
$\therefore PQ\bot PC$
$在Rt\triangle PCQ中,由勾股定理得P{C}^{2}+P{Q}^{2}=C{Q}^{2},即{2}^{2}+(m-3{)}^{2}+{m}^{2}+(n-2{)}^{2}={3}^{2}+{n}^{2}$
$整理得2{m}^{2}-6m+8=4n,即n=-\dfrac{1}{2}({m}^{2}-3m+4)=\dfrac{1}{2}{\left(m-\dfrac{3}{2}\right)}^{2}+\dfrac{7}{8}$
$\therefore m=\dfrac{3}{2}时,n取得最小值\dfrac{7}{8};$
$m=4,n取得最大值4$
$故n取值范围为\dfrac{7}{8}\leqslant n\leqslant 4$
$ $
$ $
$② 由①知:当n取得最大值4时,m=4,此时P\left(2,4\right),Q\left(4,0\right)$
$\therefore PC=\sqrt{5},PQ=2\sqrt{5},CQ=5$
$设点P到线段CQ的距离为h$
$∵{S}_{\triangle PQC}=\dfrac{1}{2}CQ\cdot h=\dfrac{1}{2}PC\cdot PQ=5$
$\therefore h=\dfrac{PC\cdot PQ}{CQ}=\dfrac{\sqrt{5}\times 2\sqrt{5}}{5}=2$
$\therefore 设点P到线段CQ的距离为2$
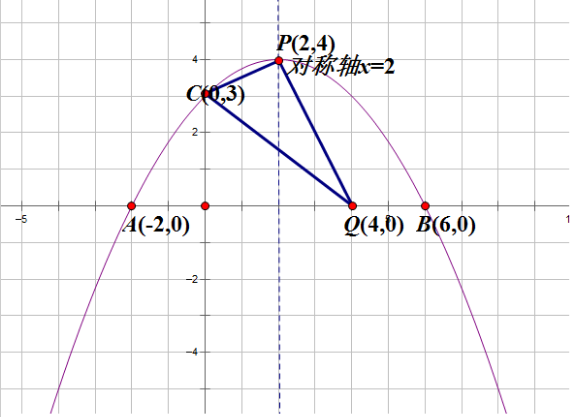
$③ 由②知:当n取得最大值4时,Q的坐标为\left(4,0\right)$
$假设CQ直线对应的函数表达式为y=ax+b\left(a\ne 0\right)$
$将C(0,3),Q\left(4,0\right)代入得\left\{\begin{array}{l}3=b\\ 0=4a+b\end{array}\right.$
$解得\left\{\begin{array}{l}a=-\dfrac{3}{4}\\ b=3\end{array}\right.$
$\therefore 直线的对应函数表达式为y=-\dfrac{3}{4}x+3$
$不妨将线段CQ向上移t个单位后其所在直线对应的函数表达式为y=-\dfrac{3}{4}x+3+t$
$当线段CQ向上平移,使点Q恰好在抛物线上,线段CQ与抛物线有两个交点,此时对应的点{Q}_{1}的纵坐标为-\dfrac{1}{4}\times (4+2)\times (4-6)=3$
$把{Q}_{1}(4,3)代入y=-\dfrac{3}{4}x+3+t,得t=3;$
$当线段CQ继续向上平移,线段CQ与抛物线只有一个交点时,联立\left\{\begin{array}{l}y=-\dfrac{1}{4}\times (x+2)\left(x-6\right)\\ y=-\dfrac{3}{4}x+3+t\end{array}\right.得{x}^{2}-7x+4t=0$
$由根的判别式{b}^{2}-4ac={\left(-7\right)}^{2}-4\times 1\times 4t=49-16t=0,得t=\dfrac{49}{16}$
$综上所述,当线段CQ与抛物线有两个交点时,t的取值范围为3\leqslant t\leqslant \dfrac{49}{16}。$
$ $