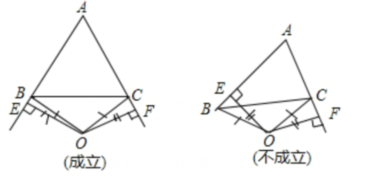
证明:$(1) $过点$ O $分别作$ O E \perp A B $于$ E$,
$O F \perp A C $于$ F$,
由题意知,
在$ R t \triangle O E B $和$ R t \triangle O F C $中
$\begin {cases}{O B=O C}\\{O E=O F}\end {cases}$
∴$R t \triangle O E B \cong R t \triangle O F C(H L)$,
∴$∠A B C=∠A C B$,
∴$A B=A C $;
$(2)$过点$ O $分别作$ O E \perp A B $于$ E$,$ O F \perp A C $于$ F$,
由题意知,$ O E=O F $,$∠B E O=∠C F O=90°$
∵在$ Rt \triangle O E B $和$Rt \triangle O F C $中
$\begin {cases}{O B=O C}\\{O E=O F}\end {cases}$
∴$Rt \triangle O E B \cong R t \triangle O F C(H L)$,
∴$∠O B E=∠O C F$,
又 ∵$O B=O C$,
∴$∠O B C=∠O C B$,
∴$∠A B C=∠A C B$,
∴$A B=A C $;
$(3)$不一定成立,$ $当$ ∠A $的平分线所在直线与边$ B C$
的垂直平分线重合时$ A B=A C$,$ $否则$ A B \neq A C.$