解$:(1)$由题意知$∠AEF=∠CEF,$
由同角或等角的余角相等得$∠AEB=∠CED.$
又因为$∠B=∠D= 90°,$
所以$△ABE∽△CDE,$
所以$\frac {AB}{CD}=\frac {BE}{DE}$
因为$BE=20\ \mathrm {m},DE=2\ \mathrm {m},CD=1.7\ \mathrm {m},$
所以$AB=17\ \mathrm {m}.$
答:建筑物$AB$的高度是$17\ \mathrm {m}.$
$(2)$因为$BD=10\ \mathrm {m},DE_1=2\ \mathrm {m},DE_2=3.4\ \mathrm {m},$
所以$BE_1= BD- DE_1=10-2= 8(\mathrm {m}),$
$BE_2= BD- DE_2=10-3.4=6. 6(\mathrm {m}).$
同理$(1)$得$△BGE_1∽△DCE _1.$
所以$\frac {BG}{DC}=\frac {BE_1}{DE_1}$
又因为$DC=1.7\ \mathrm {m},$
所以$BG=6.8\ \mathrm {m}.$
同理$(1)$得$△ABE_2∽△CDE_2,$
所以$\frac {AB}{CD}=\frac {BE_2}{DE_2}$
又因为$DC=1.7\ \mathrm {m},$
所以$AB=3.3\ \mathrm {m}.$
所以$AG= BG- AB=6.8-3.3=3.5(\mathrm {m}).$
答:这个广告牌$AG$的高度是$3.5\ \mathrm {m}.$
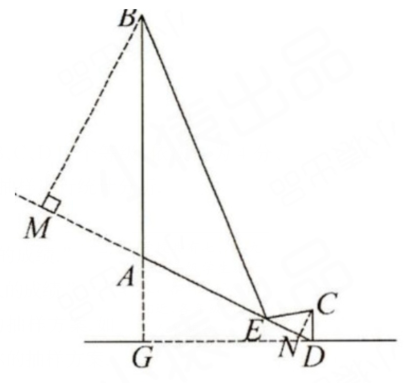
$(3)$如图,过点$C$作$CN⊥AD$于点$N,$
过点$B$作$BM⊥AD$交$DA$的延长线于点$M.$
由坡比为$8: 15($即$tan∠ADG=\frac {8}{15})$得$AG: DG=8:15,$
再由勾股定理可得$Rt△ADG$三边之比为$AG:DG:AD=8:15:17.$
得$∠AGD= ∠CDG= 90°.$
所以$∠DAG+∠ADG= 90° ,∠CDN+∠ADG= 90°,$
所以$∠CDN=∠DAG,$
所以$△DAG∽△CDN,$
所以$\frac {DA}{CD}=\frac {AG}{DN}=\frac {DG}{CN}$
所以$DN:CN:CD=8:15:17.$
又因为$CD=1.7\ \mathrm {m},$
所以$DN=0.8\ \mathrm {m},CN=1.5\ \mathrm {m}.$
因为$DE=2.8\ \mathrm {m},$
所以$NE=DE- DN=2.8-0.8=2(\mathrm {m}).$
又易证$△BME∽△CNE,$
又易证$△AMB∽△AGD,$
所以$△AMB$的三边之比$AM: BM: AB=8: 15: 17,$
所以设$AM= 8k,BM= 15k,AB= 17k.$
所以$\frac {15k}{1.5}=\frac {8k+17-2.8}{2}$
解得$k=\frac {71}{60}$
所以$AB= 17k≈20\ \mathrm {m}.$
答:信号塔$AB$的高度约是$20\ \mathrm {m}.$