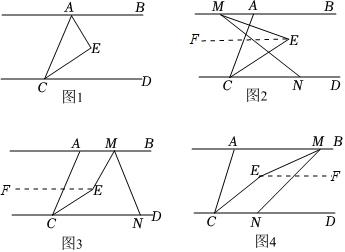
解:$(2)$如图$2,$
过点$E$作$EF∥AB,$
$∵AB∥CD,$
$∴FE∥CD,$
$∴∠BME=∠MEF,$$∠FMC=∠ECD,$
$∵ME,$$CE$分别平分$∠BMN,$$∠ACD,$
$∴∠BME=\frac {1}{2}∠BMN=22.5°,$$∠ECD=\frac {1}{2}∠ACD=35°,$
$∴∠MEC=∠MEF+∠CEF=22.5°+35°=57.5°.$
$(3)①$如图$3,$过点$E$作$EF∥AB,$
$∵AB∥CD,$
$∴FE∥CD,$
$∴∠AME+∠MEF=180°,$
$∵∠AME=\frac {1}{2}∠AMN=\frac {1}{2}α,$
$∴∠MEF=180°-\frac {1}{2}α,$
$∵∠ECD=\frac {1}{2}∠ACD=\frac {1}{2}β,$
$∴∠FEC=∠ECD=\frac {1}{2}β,$
$∴∠MEC=∠MEF+∠FEC=180°-\frac {1}{2}α+\frac {1}{2}β;$
②如图$4,$过点$E$作$EF∥AB,$
$∵AB∥CD,$
$∴FE∥CD,$
$∴∠AME=∠MEF=\frac {1}{2}α,$
$∠FEC+∠ECD=180°,$
$∵∠ECD=\frac {1}{2}∠ACD=\frac {1}{2}β,$
$∴∠FEC=180°-\frac {1}{2}β,$
$∴∠MEC=∠MEF+∠CEF=180°-\frac {1}{2}β+\frac {1}{2}α.$