电子课本网 › 第5页

第5页

信息发布者：

证明：$(1)∵DE⊥AC，$

$∴∠AHE=90°，$

$∵∠BAC=90°，$

$∴∠BAC=∠AHE=90°，$

$∴BA∥DE，$

$∴∠ABD+∠BDE=180°，$

$∵∠ABD+∠CED=180°，$

$∴∠BDE=∠CED，$

$∴BD∥EC.$

$(2)$解：如图，

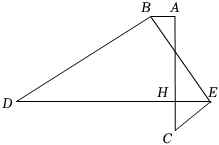
由$(1)$可得，$∠ABD+∠BDE=180°，$

$∵∠BDE=30°，$

$∴∠ABD=180°-∠BDE=180°-30°=150°，$

$∵∠DBE=∠ABE+50°，$

$∴∠ABD=∠ABE+∠DBE=∠ABE+∠ABE+50°=2∠ABE+50°=150°，$

$∴∠ABE=50°，$

$∴∠DBE=∠ABE+50°=50°+50°=100°，$

$∵BD∥EC，$

$∴∠DBE+∠CEB=180°，$

$∴∠CEB=180°-∠DBE=180°-100°=80°.$

解：$ (1) ∠AED +∠D=180°$

理由$：∵∠CED=∠GHD$

$∴CE//GF，$

$∴∠C=∠FGD$

$∵∠C=∠EFG，$

$∴∠FGD=∠EFG$

$∴AB//CD，$

$∴∠AED+∠D=180° $

$(2)∵∠DHG=∠EHF=100°，∠D=30°$

$∴∠HGD=180°-∠DHG-∠D=180°-100°-30°=50°$

$∵CE//GF，$

$∴∠C=∠HGD=50°$

$∵AB//CD，$

$∴∠AEC=∠C-50°$

$∴∠AEM=180°-∠AEC=180°-50°=130°$

上一页下一页