解$;(2)∠BFD=\frac {1}{2}∠AEC.$理由如下:
由$(1)$知:$∠AEC=∠ABC+∠ADC,$
如图,过$F$点作$FN∥AB,$
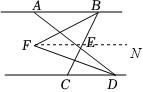
$∴∠ABF=∠BFN,$
$∵AB∥CD,$
$∴CD∥FN,$
$∴∠NFD=∠FDC,$
$∴∠BFD=∠ABF+∠FDC,$
$∵BF{平分}∠ABC,$$DF{平分}∠ADC,$
$∴∠ABF=\frac {1}{2}∠ABC,$$∠FDC=\frac {1}{2}∠ADC,$
$∴∠BFD=\frac {1}{2}(∠ABC+∠ADC)=\frac {1}{2}∠AEC.$
即$∠BFD=\frac {1}{2}∠AEC.$
$(3)∠BPD=\frac {1}{2}α-\frac {1}{6}β.$理由如下:
过$P $点作$PK∥AB,$则$PK∥AB∥CD,$
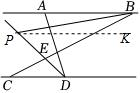
$∴∠ABP=∠BPK,$$∠CDP=∠DPK,$
$∴∠BPD=∠BPK+∠DPK=∠ABP+∠CDP,$
$∵∠ABC=β,$$∠ABP=\frac {1}{2}∠PBC,$
$∴∠ABP=\frac {1}{3}∠ABC=\frac {1}{3}β,$
$∵AB∥CD,$
$∴∠DCE=∠ABC=β,$
$∴∠ADC=∠AEC-∠DCE=α-β,$
$∴∠CDP=\frac {1}{2}∠ADC=\frac {1}{2}α-\frac {1}{2}β,$
$∴∠BPD=∠ABP+∠CDP=\frac {1}{3}β+\frac {1}{2}α-\frac {1}{2}β=\frac {1}{2}α-\frac {1}{6}β$
同理,当点$P$在$AB$上方时,$∠BPD=\frac {α-3β}{2},$
综上,$∠BPD=\frac {1}{2}α-\frac {1}{6}β$或$\frac {α-3β}{2}.$