解:$(2)$∵$∠MAN=∠BAD=30°$
∴当$△AMN$中有两个角相等时
分类讨论如下:
①
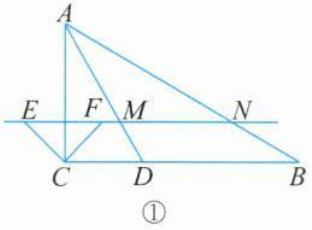
如图①,当$∠ANM=∠MAN=30°$时,
$∠AME=∠MAN +∠ANM=60°$
∵$∠ADC=60°$
∴$∠AME=∠ADC$
∴$EM//CD$
∴$∠DCF=∠CFE=45°$
∴$CE$旋转了$45°;$
②
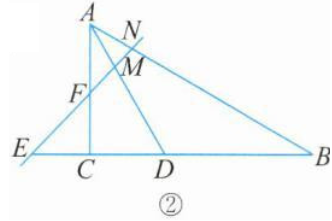
如图②,当$∠AMN=∠ANM,$且点$F $在直线$BC$上方时,
$∠AMN=∠ANM=\frac {1}{2} (180°-∠MAN)=75°$
∴$∠DMF=∠AMN=75°$
∵$∠CFM=135°$
∴$∠DCF=360°-∠DMF-∠ADC-∠CFM=90°$
∴$CE$旋转了$90°;$
③
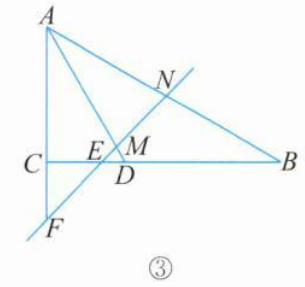
如图③,当$∠AMN=∠ANM=75°,$且点$F $在直线$BC$下方时,
$∠AME=180°-∠AMN=105°$
∵$∠CEF=45°$
∴$∠CEM=180°-∠CEF=135°$
∵$∠CAD=30°$
∴$∠ACE=360°-∠CAD-∠AME-∠CEM=90°$
∴$CE$旋转了$360°-90°=270°;$
④
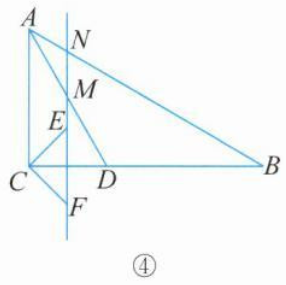
如图④,当$∠AMN=∠MAN=30°$时,$∠DMF=∠AMN=30°$
∴$∠DMF=∠CAD$
∴$AC//FN$
∴$∠ACE=∠CEF=45°$
∴$CE$旋转了$360°-45°=315°.$
综上所述,当$CE$旋转$45°$或$90°$或$270°$或$315°$时,$△AMN$中有两个角相等