电子课本网 › 第23页

第23页

信息发布者：

半径

这条半径

唯一

圆心

C

相切

相切

证明:连接$OD$

$∵D$是$AC$的中点

$∴AD=DC$

$∵AO=OB$

$∴OD$是$△ABC$的中位线

$∴OD//BC$

$∴∠HDO=∠HGB$

$∵HG⊥BC$

$∴∠HGB=90°$

$∴∠HDO=90°$

即$OD⊥HG$

$∵OD$是$⊙O$的半径

$∴HG$是$⊙O$的切线.

证明：连接OA，如图，

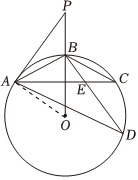
$∵AB=BC，$

$∴∠BAC=∠BCA.$

$∵∠PAB=∠ACB，$

$∴∠BAC=∠PAB.$

$∵AB=BC，$

$∴\widehat{AB}=\widehat{AC}$

$∴OB⊥AC，$

$∴∠BAC+∠ABO=90°，$

$∵OB=OA，$

$∴∠ABO=∠BAO.$

$∴∠BAO+∠∠BAC=90°，$

$∴∠BAO+∠PAB=90°，$

$∴∠PAO=90°，$

即$OA⊥AP，$

$∵OA$为$⊙O$的半径，

$∴AP$是$⊙O$的切线.

上一页下一页