证明:$(1)∵∠BAC$的平分线交$△ABC$的外接圆于点$D,$$∠ABC$的平分线交$AD$于点$E,$
$∴∠BAD=∠CAD,$$∠ABE=∠CBE.$
$∵∠CAD=∠CBD,$
$∴∠BAD=∠CAD=∠CBD.$
$∵∠BED=∠ABE+∠BAD=∠CBE+∠CBD,$
即$∠BED=∠DBE,$
$∴DB=DE.$
$(2)$连接$CD.$
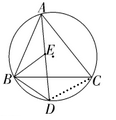
∵∠BAC=90°,
$∴BC$是$△ABC$外接圆的直径,
$∴∠BDC=90°.$
$∵∠CAD=∠BAD=∠CBD,$$∠BAC=90°,$
$∴∠CBD=45°,$
$∴△BCD$是等腰直角三角形,
$∴BC=\sqrt{2}BD=4\sqrt{2},$
$∴△ABC$外接圆的半径为$2\sqrt{2}.$