电子课本网 › 第51页

第51页

信息发布者：

解：$(1)∵∠A+∠ABC+∠ACB=180°，$

$∴∠ABC+∠ACB=180°-∠A=180°-∠A，$

$∵BO$平分$∠ABC，$$CO$平分$∠ACB，$

$∴∠OBC+∠OCB=\frac {1}{2}∠ABC+\frac {1}{2}∠ACB=\frac {1}{2}(∠ABC+∠ACB)$

$=\frac {1}{2}×(180°-∠A)=90°-\frac {1}{2}∠A，$

$∴∠BOC=180°-(∠OBC+∠OCB)=90°+\frac {1}{2}∠A=90°+40°=130°.$

$(2)∵BO$平分$∠ABC，$

$∴∠ABO=∠CBO，$

$∵MN∥BC，$

$∴∠MOB=∠CBO，$

$∴∠ABO=∠MOB，$

$∴MO=BM，$

同理可得，$NO=NC，$

$∴AM+MN+AN=AM+MO+ON+AN=AM+BM+AN+NC=AB+AC，$

$∵AB=5，$$AC=7，$

$∴AB+AC=12，$

$∴△AMN$的周长$=AB+AC=12.$

解：$(1)∵∠A=60°，$

$∴∠ABC+∠ACB=180°-∠A=120°，$

$∵BE$平分$∠ABC，$$CF_{平分}∠ACB，$

$∴∠ABE=∠CBE=\frac {1}{2}∠ABC，$$∠BCF=∠ACF=\frac {1}{2}∠ACB，$

$∴∠CBE+∠BCF=\frac {1}{2}∠ABC+\frac {1}{2}∠ACB=\frac {1}{2}×120°=60°，$

$∴∠BPC=180°-(∠CBE+∠BCF)=180°-60°=120°.$

(2)证明：在BC上截取BQ=BF，连接PQ，

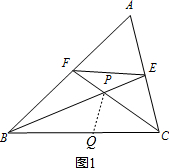
在$△FBP $和$△QBP $中，

$\begin{cases}{BP=BP}\\{∠FBP=∠QBP}\\{BF=BQ}\end{cases}$

$∴△FBP≌△QBP(\mathrm {SAS})，$

$∴FP=QP，$$∠BFP=∠BQP，$

$∵∠A=60°，$$∠FPE=∠BPC=120°，$

$∴∠AFP+∠AEP=360°-60°-120°=180°，$

$∴∠BFP+∠CEP=180°，$

$∵∠CQP+∠BQP=180°，$

$∴∠CEP=∠CQP，$

在$△CQP $和$△CEP $中，

$\begin{cases}{∠QCP=∠ECP}\\{∠CQP=∠CEP}\\{CP=CP}\end{cases}$

$∴△CQP≌△CEP(\mathrm {AAS})，$

$∴EF=QP，$

$∵FP=QP，$

$∴FP=EP，$

$∴△EFP$是等腰三角形.