证明:$(1)$连接$AD,$
$∵AB=AC,$$∠BAC=90°,$$D$为$BC$的中点,
$∴AD⊥BC,$$BD=AD,$
$∴∠B=∠BAD=∠DAC=45°.$
$∵BE=AF,$$∠B=∠DAC,$$BD=AD,$
$∴△BDE≌△ADF,$
$∴ED=FD,$$∠BDE=∠ADF,$
$∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°,$
$∴△DEF$为等腰直角三角形.
$(2)△DEF$为等腰直角三角形.
证明:连接$AD.$
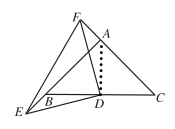
∵AB=AC,
$∴△ABC$为等腰三角形.
$∵∠BAC=90°,$$D$为$BC$的中点,
$∴AD=BD,$$AD⊥BC,$
$∴∠DAC=∠ABD=45°,$
$∴∠DAF=∠DBE=135°.$
又$AF=BE,$
$∴△DAF≌△DBE,$
$∴FD=ED,$$∠FDA=∠EDB,$
$∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°,$
$∴△DEF$仍为等腰直角三角形.