解:$(1)△DEF$是等边三角形,
理由如下:$∵AB=AD,$$∠A=60°,$
$∴△ABD$是等边三角形,
$∴∠ABD=∠ADB=60°,$
$∵CE∥AB,$
$∴∠CED=∠A=60°,$$∠DFE=∠ABD=60°,$
$∴∠CED=∠ADB=∠DFE,$
$∴△DEF$是等边三角形.
$(2)$连接$AC$交$BD$于点$O,$
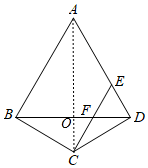
$∵AB=AD,$$CB=CD,$
$∴AC$是$BD$的垂直平分线,
即$AC⊥BD,$
$∵AB=AD,$$∠BAD=60°,$
$∴∠BAC=∠DAC=30°,$
$∵CE∥AB,$
$∴∠BAC=∠ACE=∠CAD=30°,$
$∴AE=CE=8,$
$∴DE=AD-AE=12-8=4,$
$∵△DEF$是等边三角形,
$∴EF=DE=4,$
$∴CF=CE-EF=8-4=4.$