解:$(1)△ABC$与$△ACD,$$△ABC$与$△CBD$是“等角三角形”.
$(2)$证明:∵在$△ABC$中,$∠A=40°,$$∠B=60°,$
$∴∠ACB=180°-∠A-∠B=80°,$
$∵CD$为角平分线,
$∴∠ACD=∠DCB=\frac {1}{2}∠ACB=40°,$
$∴∠ACD=∠A,$$∠DCB=∠A,$
$∴CD=DA,$
在$△DBC$中,$∠DCB=40°,$$∠B=60°,$
$∴∠BDC=180°-∠DCB-∠B=80°,$
$∴∠BDC=∠ACB,$
$∵CD=DA,$$∠BDC=∠ACB,$$∠DCB=∠A,$
$∠B=∠B,$
$∴CD$为$△ABC$的等角分割线.
$(3)$解:当$△ACD$是等腰三角形,如图$2,$$DA=DC$时,$∠ACD=∠A=40°,$
$∴∠ACB=∠BDC=40°+40°=80°,$
$∴∠B=180°-∠A-∠ACB=60°;$
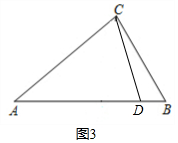
当$△ACD$是等腰三角形,如图$3,$$DA=AC$时,$∠ACD=∠ADC=70°,$
$∠BCD=∠A=40°,$
$∴∠ACB=70°+40°=110°,$
$∴∠B=180°-∠A-∠ACB=30°;$
当$△ACD$是等腰三角形,$CD=AC$的情况不存在,
当$△BCD$是等腰三角形,如图$4,$$DC=BD$时,$∠ACD=∠BCD=∠B,$
$∵∠A+∠B+∠ACB=180°,$
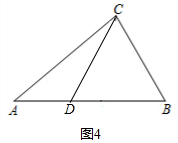
$∴∠B=\frac {180°-40°}{3}=(\frac {140}{3})°,$
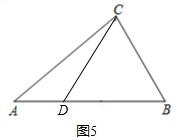
当$△BCD$是等腰三角形,如图$5,$$DB=BC$时,$∠BDC=∠BCD,$
设$∠BDC=∠BCD=x,$
则$∠B=180°-2x,$
则$∠ACD=∠B=180°-2x,$
由题意得,$180°-2x+40°=x,$
解得$x=(\frac {220}{3})°,$
$∴∠B=180°-2x=(\frac {100}{3})°,$
当$△BCD$是等腰三角形,$CD=CB$的情况不存在,
综上,$∠B$的度数为$60°;$$30°;$$(\frac {140}{3})°;$$(\frac {100}{3})°.$