解:(1)$a = 8\div50 = 0.16,$$b = 12\div50 = 0.24,$
$c = 50×0.2 = 10,$$d = 50×0.04 = 2。$
补全频数分布直方图。
(2)$37800×(0.2 + 0.06 + 0.04)=11340$(名)。
答:估计日行走步数超过12000(包含12000)的教师有11340名。
(3)设步数$x$满足$16000\leq x<20000$的3名教师分别为A、B、C,
步数$x$满足$20000\leq x<24000$的2名教师分别为X、Y,
画树状图如下:
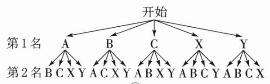
由树状图可知,随机选取日行走步数超过$16000($包含$16000)$
的$2$名教师共有$20$种等可能的结果,其中被选取的$2$名教师日
行走步数恰好都在$20000$以上$($包含$20000)$的有$(X,$$Y)、$$(Y,$$X)$这$2$种结果,
所以被选取的2名教师日行走步数恰好都在20000以上(包含
20000)的概率为$\frac{2}{20}=\frac{1}{10}。$