解:(1)如图,
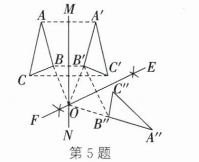
(2)$\angle BOB'' = 2\alpha。$
理由:如图,连接$BO,$$B'O,$$B''O。$
因为$\triangle ABC$和$\triangle A'B'C'$关于直线$MN$对称,所以$\angle BOM = \angle B'OM。$
又因为$\triangle A'B'C'$和$\triangle A''B''C''$关于直线$EF$对称,所以$\angle B'OE = \angle B''OE。$
所以$\angle BOB'' = \angle BOM + \angle B'OM + \angle B'OE + \angle B''OE = 2(\angle B'OM + \angle B'OE)=2\alpha,$即$\angle BOB'' = 2\alpha。$