电子课本网 › 第4页

第4页

信息发布者：

$15^{\circ}$

 解：（2）①$\triangle ABD$是“准互余三角形”。理由：

因为$AD$是$\triangle ABC$的角平分线，

所以$\angle BAC = 2\angle BAD。$

因为$\angle ACB = 90^{\circ}，$所以$\angle BAC+\angle B = 90^{\circ}。$

所以$2\angle BAD+\angle B = 90^{\circ}。$

所以$\triangle ABD$是“准互余三角形”。

 ②因为$\triangle ABE$是“准互余三角形”，且$\angle AEB=\angle ACB+\angle EAC\gt90^{\circ}，$

所以$2\angle EAB+\angle ABC = 90^{\circ}$或$\angle EAB+2\angle ABC = 90^{\circ}。$

因为$\angle ABC = 24^{\circ}，$所以$\angle EAB = 42^{\circ}$或$\angle EAB = 33^{\circ}。$

 当$\angle EAB = 42^{\circ}，$$\angle ABC = 24^{\circ}$时，$\angle AEB = 114^{\circ}，$

所以$\angle EAC=\angle AEB-\angle ACB = 24^{\circ}。$

 当$\angle EAB = 33^{\circ}，$$\angle ABC = 24^{\circ}$时，$\angle AEB = 123^{\circ}，$

所以$\angle EAC=\angle AEB-\angle ACB = 33^{\circ}。$

 所以$\angle EAC$的度数为$33^{\circ}$或$24^{\circ}。$

124

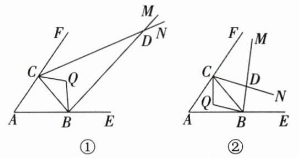
解：$(2) ①$当点$ Q $在$ BC $上方时，如图①.

∵$∠EAF = 56°，$$∠CQB = 104°，$

∴$∠ACQ + ∠ABQ = 180 + 180 - (56° + 104°) = 200°.$

∴$∠FCQ + ∠QBE = 360 - (∠ACQ + ∠ABQ) = 160°.$

∵$BM，$$CN $分别平分$∠QBE，$$∠QCF，$

∴$∠DCQ + ∠QBD = \frac {1}{2}(∠FCQ + ∠QBE) = 80°.$

∵$∠QCB + ∠CBQ = 180 - ∠CQB = 76°，$

∴$∠DCB + ∠DBC = ∠QCB + ∠DCQ + ∠CBQ + ∠QBD$

$ = (∠DCQ + ∠QBD) + (∠QCB + ∠CBQ) $

$= 80° + 76° = 156°.$

∴$∠BDC = 180 - (∠DCB + ∠DBC) = 180 - 156° = 24°.$

$②$当点$ Q $在$ BC $下方时，如图②.

∵$∠ACB + ∠ABC = 180 - ∠EAF = 124°，$

∴$∠FCB + ∠EBC = 360 - 124° = 236°.$

又∵$∠CQB = 104°，$

∴$∠QCB + ∠QBC = 180 - 104° = 76°.$

∴$∠FCQ + ∠QBE = 236° + 76° = 312°.$

又∵$BM，$$CN $分别平分$∠QBE $和$∠QCF，$

∴$∠DCQ + ∠DBQ = \frac {1}{2}×312° = 156°.$

∴$∠BDC = 180 + 180 - 104° - 156° = 100°.$

综上所述，$∠BDC $的度数为$ 24°$或$ 100°$

$(3) ∠AOG - \frac {1}{2}∠ACG = 45°$