电子课本网 › 第7页

第7页

信息发布者：

6或8

解：图中共有 3 对全等三角形，分别是$\triangle ABF\cong \triangle DEC$，

$\triangle ABC\cong \triangle DEF$，$\triangle BCF\cong \triangle EFC$。答案不唯一，

如选择$\triangle ABF\cong \triangle DEC$。理由：

$∵AB// DE$，$∴∠A=∠D$。

在$\triangle ABF$和$\triangle DEC$中，

$\{\begin {array}{l}AB = DE，\\∠A=∠D，\\AF = DC，\end {array}.$

$∴\triangle ABF\cong \triangle DEC$。

一

 解：（1）小星的解答从第一步开始出现错误。
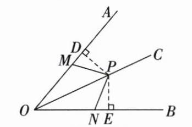
 （2）证明：如图，过点$P$作$PD\perp OA$于点$D，$$PE\perp OB$于点$E。$
 因为$PD\perp OA，$$PE\perp OB，$所以$\angle PDM=\angle PEN = 90^{\circ}。$
 因为$\angle PMO=\angle PNO，$$\angle PMD = 180^{\circ}-\angle PMO，$
$\angle PNE = 180^{\circ}-\angle PNO，$
 所以$\angle PMD=\angle PNE。$
 在$\triangle PMD$和$\triangle PNE$中，
 $\begin{cases}\angle PDM=\angle PEN\\\angle PMD=\angle PNE\\PM = PN\end{cases}，$
 所以$\triangle PMD\cong\triangle PNE(AAS)，$所以$PD = PE。$
 因为$PD\perp OA，$$PE\perp OB，$所以$OC$是$\angle AOB$的平分线。