电子课本网 › 第8页

第8页

信息发布者：

 证明：（1）因为$PM\perp AC，$$QN\perp AC，$
所以$\angle PMA=\angle QNC = 90^{\circ}。$
 在$Rt\triangle APM$和$Rt\triangle CQN$中，
 $\begin{cases}PA = QC\\PM = QN\end{cases}，$
 所以$Rt\triangle APM\cong Rt\triangle CQN(HL)。$
 （2）由（1）知$\triangle APM\cong\triangle CQN，$所以$AM = CN。$
 在$\triangle PMD$和$\triangle QND$中，
 $\begin{cases}\angle PMD=\angle QND = 90^{\circ}\\\angle PDM=\angle QDN\\PM = QN\end{cases}，$
 所以$\triangle PMD\cong\triangle QDN(AAS)，$所以$DM = DN。$
 所以$DM = CD + CN = CD + AM。$
 又因为$DM+CD+AM = AC，$所以$DM+DM = AC，$
即$DM=\frac{1}{2}AC。$

 证明：（1）在$\triangle ABD$和$\triangle ACE$中，
 $\begin{cases}AB = AC\\\angle 1=\angle 2\\AD = AE\end{cases}，$
 所以$\triangle ABD\cong\triangle ACE(SAS)，$所以$BD = CE。$
 （2）因为$\angle 1=\angle 2，$所以$\angle 1+\angle DAE=\angle 2+\angle DAE，$
即$\angle BAN=\angle CAM。$
 由（1）知$\triangle ABD\cong\triangle ACE，$所以$\angle B=\angle C。$
 在$\triangle ACM$和$\triangle ABN$中，
 $\begin{cases}\angle C=\angle B\\AC = AB\\\angle CAM=\angle BAN\end{cases}，$
 所以$\triangle ACM\cong\triangle ABN(ASA)，$所以$\angle M=\angle N。$

 （1）①证明：因为$\angle ADE=\angle C = 90^{\circ}，$

所以$\angle EDB+\angle ADC = 90^{\circ}，$$\angle A+\angle ADC = 90^{\circ}，$

所以$\angle EDB=\angle A。$

 ②证明：在$AC$上截取$CF = CD，$连接$FD。$

 因为$\angle C = 90^{\circ}，$$CF = CD，$

所以$\angle CFD=\angle CDF = 45^{\circ}，$

则$\angle AFD = 180^{\circ}-45^{\circ}=135^{\circ}。$

 又因为$\angle DBE = 135^{\circ}，$所以$\angle AFD=\angle DBE。$

 因为$AC = BC，$$CF = CD，$

所以$AC - CF = BC - CD，$即$AF = BD。$

 在$\triangle AFD$和$\triangle DBE$中，

 $\begin{cases}\angle A=\angle EDB\\AF = BD\\\angle AFD=\angle DBE\end{cases}，$

 所以$\triangle AFD\cong\triangle DBE(ASA)，$所以$DA = DE。$

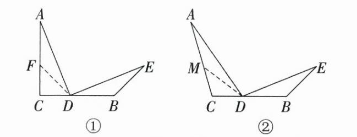
 （2）当$DA = DE$时，$\angle DBE = 90^{\circ}+\frac{1}{2}\angle C。$

 理由：在$AC$上截取$CM = CD，$连接$MD。$

 因为$AC = BC，$所以$AC - CM = BC - CD，$即$AM = DB。$

 因为$\angle ADB=\angle A+\angle C，$$\angle ADB=\angle ADE+\angle EDB，$且$\angle ADE=\angle C，$所以$\angle A=\angle EDB。$

 在$\triangle AMD$和$\triangle DBE$中，

 $\begin{cases}DA = DE\\\angle A=\angle EDB\\AM = DB\end{cases}，$

 所以$\triangle AMD\cong\triangle DBE(SAS)，$所以$\angle AMD=\angle DBE。$

 因为$CM = CD，$

所以$\angle CMD=\angle CDM=\frac{180^{\circ}-\angle C}{2}=90^{\circ}-\frac{1}{2}\angle C。$

 又因为$\angle AMD = 180^{\circ}-\angle CMD，$

所以$\angle AMD = 180^{\circ}-(90^{\circ}-\frac{1}{2}\angle C)=90^{\circ}+\frac{1}{2}\angle C，$

所以$\angle DBE = 90^{\circ}+\frac{1}{2}\angle C。$