电子课本网 › 第12页

第12页

信息发布者：

解： (1) 

 (2) 解：连接$DB，$$DC。$

 由题意，得$DB = DC。$

 因为$AD$平分$\angle CAB，$$DM\perp AB，$$DN\perp AC，$所以$DM = DN，$$\angle DAB=\angle DAC。$

 在$\triangle DAM$和$\triangle DAN$中，

$\begin{cases}\angle DMA=\angle DNA\\\angle DAM=\angle DAN\\DA = DA\end{cases}，$

所以$\triangle DAM\cong\triangle DAN，$所以$AM = AN。$

 在$Rt\triangle DBM$和$Rt\triangle DCN$中，

$\begin{cases}DB = DC\\DM = DN\end{cases}，$

所以$Rt\triangle DBM\cong Rt\triangle DCN，$所以$BM = CN，$

即$AB - AM = AN - AC，$

所以$AB - AM = AM - AC，$

所以$AM=\frac{1}{2}(AB + AC)=\frac{1}{2}\times(8 + 6)=7。$

 (1) 证明：因为$AB = AC，$所以$\angle ABC=\angle ACB。$

 在$\triangle BCD$和$\triangle CBE$中，

$\begin{cases}BC = CB\\\angle DBC=\angle ECB\\BD = CE\end{cases}，$

所以$\triangle BCD\cong\triangle CBE，$

所以$\angle FBC=\angle FCB，$所以$BF = CF。$

 (2) 解：因为$AB = AC，$$\angle BAC = 45^{\circ}，$

所以$\angle ABC=\angle ACB=\frac{1}{2}(180^{\circ}-\angle BAC)=67.5^{\circ}。$

由

 (1)知$\angle FBC=\angle FCB，$

所以易得$\angle FBD=\angle ECF。$

 设$\angle FBD=\angle ECF = x，$

则$\angle FBC=\angle FCB = 67.5^{\circ}-x，$
$\angle BDF=\angle ECF+\angle BAC=x + 45^{\circ}，$
$\angle DFB = 2\angle FBC = 2(67.5^{\circ}-x)=135^{\circ}-2x。$

 因为$\triangle BFD$是等腰三角形，分三种情况讨论：

 ①当$BD = BF$时，$\angle BDF=\angle DFB，$

所以$x + 45^{\circ}=135^{\circ}-2x，$

解得$x = 30^{\circ}，$即$\angle FBD = 30^{\circ}；$

 ②当$BD = DF$时，$\angle FBD=\angle DFB，$

所以$x = 135^{\circ}-2x，$

解得$x = 45^{\circ}，$即$\angle FBD = 45^{\circ}；$

 ③当$BF = DF$时，$\angle FBD=\angle FDB，$

所以$x = x + 45^{\circ}，$不符合题意，舍去。

 综上所述，$\angle FBD = 30^{\circ}$或$45^{\circ}。$

 解：(1) 证明：在$Rt\triangle ABC$中，$\angle ACB = 90^{\circ}，$$\angle A = 30^{\circ}，$

所以$\angle ABC = 60^{\circ}，$$BC=\frac{1}{2}AB。$

 因为$BD$平分$\angle ABC，$所以$\angle CBD=\angle DBA=\angle A = 30^{\circ}，$

所以$AD = BD。$

 因为$DE\perp AB，$所以$AE = BE=\frac{1}{2}AB，$

所以$BC = BE，$所以$\triangle EBC$是等边三角形。

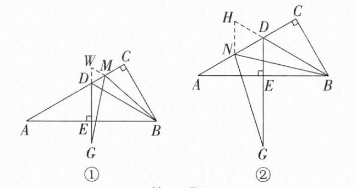
 (2) 画出完整图形如图①所示，$AD = DG + DM。$

 如图①，延长$ED$至点$W，$使得$DW = DM，$连接$MW。$

由

 (1)，易得$\angle ADE=\angle BDE = 60^{\circ}，$所以$\angle MDB = 60^{\circ}，$
$\angle WDM=\angle ADE = 60^{\circ}。$

 又因为$DM = DW，$所以$\triangle WDM$是等边三角形，

所以$DW = WM = DM，$$\angle W=\angle WMD = 60^{\circ}，$

所以$\angle W=\angle MDB。$

 因为$\angle BMG = 60^{\circ}，$

所以$\angle WMD+\angle DMG=\angle BMG+\angle DMG，$

即$\angle WMG=\angle DMB。$

 在$\triangle WGM$和$\triangle DBM$中，

$\begin{cases}\angle W=\angle MDB\\WM = DM\\\angle WMG=\angle DMB\end{cases}，$

所以$\triangle WGM\cong\triangle DBM，$所以$WG = DB。$

由

 (1)得$AD = BD，$因为$WG = DG + DW = DG + DM，$

所以$AD = DG + DM。$

 (3) $AD = DG - DN。$

 理由：如图②，延长$BD$至点$H，$使得$DH = DN，$连接$HN。$

由

 (2)，得$\angle ADE = 60^{\circ}，$$\angle CDB = 60^{\circ}，$

所以$\angle HDN=\angle CDB = 60^{\circ}。$

 又因为$DH = DN，$所以$\triangle DHN$为等边三角形，

所以$HN = DN = HD，$$\angle H=\angle HND = 60^{\circ}，$

所以$\angle H=\angle NDG。$

 因为$\angle BNG = 60^{\circ}，$

所以$\angle HND+\angle DNB=\angle BNG+\angle DNB，$即$\angle HNB=\angle DNG。$

 在$\triangle DNG$和$\triangle HNB$中，

$\begin{cases}\angle DNG=\angle HNB\\DN = HN\\\angle NDG=\angle H\end{cases}，$

所以$\triangle DNG\cong\triangle HNB，$所以$DG = HB。$

 因为$HB = HD + BD = DN + BD，$

且$AD = BD，$所以$DG = DN + AD，$

即$AD = DG - DN。$