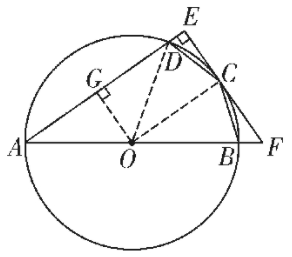
$(1)$证明:连接$OC$
∵$OB=OC$
∴$∠OCB=∠OBC$
∵四边形$ABCD$内接于$⊙O$
∴$∠OBC+∠ADC=180°$
∵$∠ADC+∠CDE=180°$
∴$∠CDE=∠OBC$
∵$CE⊥AD$
∴$∠E=∠CDE+∠ECD=90°$
∵$∠ECD=∠BCF$
∴$∠OCB+∠BCF=90°$
∴$∠OCE=90°,$即$OC⊥EF$
∵$OC$是$⊙O$的半径
∴$CE$为$⊙O$的切线
$(2)$解:如图,过点$O$作$OG⊥AE$于$G,$连接$OC,$$OD,$则$∠OGE=90°$
∵$∠E=∠OCE=90°$
∴四边形$OGEC$是矩形
∴$OC=EG,$$OG=EC$
设$⊙O$的半径为$x$
在$Rt△CDE$中,$CD=3,$$DE=1$
∴$EC=\sqrt {3^2-1^2}=2\sqrt {2}$
∴$OG=2\sqrt {2},$$GD=x-1,$$OD=x$
由勾股定理得:$OD^2=OG^2+DG^2$
∴$x^2=(2\sqrt {2})^2+(x-1)^2$
解得:$x=4.5$
∴$⊙O$的半径是$4.5$