证明:$(1)∵E$是$△ABC$的内心,
$∴∠BAE=∠CAE,$$∠EBA=∠EBC,$
$∵∠BED=∠BAE+∠EBA,$$∠DBE=∠EBC+∠DBC,$$∠DBC=∠EAC,$
$∴∠DBE=∠DEB,$
$∴DB=DE.$
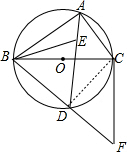
$(2)$连接$CD.$
$∵DA$平分$∠BAC,$
$∴∠DAB=∠DAC,$
$∴\widehat{BD}=\widehat{CD},$
$∴BD=CD,$
$∵BD=DF,$
$∴CD=DB=DF,$
$∴∠BCF=90°,$
$∴BC⊥CF,$
$∴CF$是$⊙O$的切线.