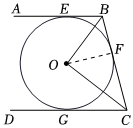
解:$(1)$连接$OF$
根据切线长定理得:
$BE=BF,$$CF=CG,$$∠OBF=∠OBE,$$∠OCF=∠OCG.$
$∵AB∥CD,$
$∴∠ABC+∠BCD=180°,$
$∴∠OBF+∠OCF=90°,$
$∴∠BOC=90°$
$∴△OBC$是直角三角形。
$(2)∵BC$与$⊙O$相切于点$F,$
$∴OF⊥BC,$
$∴S_{△OBC}=\frac {1}{2}OF×BC=\frac {1}{2}OB×OC,$
即$\frac {1}{2}OF×10=\frac {1}{2}×6×8.$
$∴OF=4.8.$