第16页 - 通城学典课时作业本八年级数学人教版南通专版

110°

$\frac {1}{2}α$

解：$(1) ∵ AD⊥BC，$

$∴ ∠ADC=90°. $

$∵ AE$平分$∠BAC，$

$∴ ∠EAC= \frac {1}{2} ∠BAC. $

$∵ ∠BAC=180°-∠B-∠C，$

$∴ ∠EAC=90°- \frac {1}{2} ∠B- \frac {1}{2} ∠C. $

$∵ ∠DAC=90°-∠C，$

$∴ ∠DAE=∠DAC-∠EAC=90°-∠C-(90°- \frac {1}{2} ∠B-\frac {1}{2} ∠C= \frac {1}{2} (∠B-∠C). $

$∵ ∠B-∠C=30°，$

$∴ ∠DAE=\frac {1}{2} ×30°=15°$

解：$(1)∵∠A=80°.$

$∴∠ABC+∠ACB=100°，$

∵点$P$是$∠ABC$和$∠ACB$的平分线的交点，

$∴∠P=180°-\frac {1}{2}(∠ABC+∠ACB)=180°-\frac {1}{2}×100°=130°.$

$(2)∵$外角$∠MBC，$$∠NCB$的角平分线交于点$Q，$

$∴∠QBC+∠QCB=\frac {1}{2}(∠MBC+∠NCB)$

$=\frac {1}{2}(360°-∠ABC-∠ACB)$

$=\frac {1}{2}(180°+∠A)$

$=90°+\frac {1}{2}∠A$

$∴∠Q=90°-\frac {1}{2}∠A.$

$(3)∵CQ$为$△ABC$的外角$∠NCB$的角平分线，

$∴CE$是$△ABC$的外角$∠ACF$的平分线，

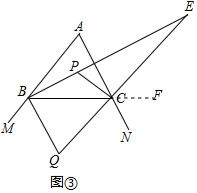
$∴∠ACF=2∠ECF，$

$∵BE$平分$∠ABC，$

$∴∠ABC=2∠EBC，$

$∵∠ECF=∠EBC+∠E，$

$∴2∠ECF=2∠EBC+2∠E，$

即$∠ACF=∠ABC+2∠E，$

又$∵∠ACF=∠ABC+∠A，$

$∴∠A=2∠E，$即$∠E=\frac {1}{2}∠A；$

$∵∠EBQ=∠EBC+∠CBQ$

$=\frac {1}{2}∠ABC+\frac {1}{2}∠MBC$

$=\frac {1}{2}(∠ABC+∠A+∠ACB)=90°.$

如果$△BQE$中，存在一个内角等于另一个内角的$2$倍，那么分四种情况：

$①∠EBQ=2∠E=90°，$则$∠E=45°，$$∠A=2∠E=90°；$

$②∠EBQ=2∠Q=90°，$则$∠Q=45°，$$∠E=45°，$$∠A=2∠E=90°；$

$③∠Q=2∠E，$则$90°-\frac {1}{2}∠A=∠A，$解得$∠A=60°；$

$④∠E=2∠Q，$则$\frac {1}{2}∠A=2(90°-\frac {1}{2}∠A)，$解得$∠A=120°.$

综上所述，$∠A$的度数是$90°$或$60°$或$120°.$