第33页 - 通城学典课时作业本八年级数学人教版南通专版

C

2

证明$：(1)$过点$C$作$CF⊥AB，$交$AB$的延长线于点$F. $

$∵ CE⊥AD， $

$∴ ∠DEC=∠BFC=90°$

$∵ ∠D+∠ABC=180°，∠CBF+∠ABC=180°， $

$∴ ∠D=∠CBF.$

在$△CDE$和$△CBF $中，

$\begin{cases}{∠D=∠CBF}\\{∠DEC=∠BFC，}\\{CD=CB}\end{cases}$

$∴ △CDE≌△CBF. $

$∴ CE=CF.$

又$∵ CE⊥AD，CF⊥AB， $

$∴ AC$平分$∠DAB$

$(2)$由$(1)，$可得$BF=DE=4.$

在$Rt△ACE$和$Rt△ACF $中，

$AC=AC$

$CE=CF，$

$∴ Rt∠ACE≌Rt△ACF. $

$∴ AE=AF=10. $

$∴ AB=AF-BF=6$

解：$(1)$如图，过点$P$作$PD⊥BD、$$PE⊥BE、$$PF⊥AC；$

$∵∠ACD$的平分线$CP$与$∠ABC$平分线$BP$交于点$P，$

$∴PD=PE，$$PD=PF，$

$∴PE=PF，$

$∴PA$平分$∠CAE.$

$(2)$设$∠ABC=2α，$$∠ACD=2β；$

$∵∠ACD$的平分线$CP$与$∠ABC$平分线$BP$交于点$P，$

$∴β=α+∠BPC，$而$β=\frac {2α+∠BAC}{2}，$

$∴∠BAC=2∠BPC=80°，$

$∴∠CAP=\frac {180°-80°}{2}=50°.$

解：$(1)∵∠BAD=100°，$

$∴∠DAF=180°-∠BAD=80°，$

$∵EF⊥AB，$

$∴∠AFE=90°，$

$∴∠EAE+∠AEF=90°，$

$∴∠EAF=90°-∠AEF=90°-50°=40°，$

$∴∠CAD=∠DAF-∠EAF=80°-40°=40°.$

$(2)$证明：如图所示，过点$E$作$EN⊥AD$于点$N，$$EM⊥CD$于点$M，$

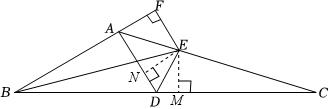
$∵∠ABC$的平分线交$AC$于点$E，$$EM⊥CD，$$EF⊥AB，$

$∴EM=EF，$

由$(1)$可得，$∠CAD=∠CAF=40°，$

$∴CA$平分$∠DAF，$

又$∵EN⊥AD，$$EF⊥AF，$

$∴EF=EN，$

$∴EM=EN，$

$∵EN⊥AD，$$EM⊥CD，$

$∴DE$平分$∠ADC.$

$(3)$解：由$(2)$可知，$EF=EN=EM，$

$∵S_{△ADE}+S_{△CDE}=S_{△ACD}，$

$∴\frac {1}{2}•AD•EN+\frac {1}{2}•CD•EM=15，$即$2EF+4EF=15，$

$∴EF=\frac {5}{2}，$

$∴S_{△ABE}=\frac {1}{2}•AB•EF=\frac {35}{4}.$