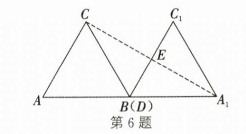
解:如图,连接$CA_1,$交$BC_1$于点$E.$
$∵△ABC$与$△A_1BC_1$是两个全等的等边三角形,
$∴ BA=BC=BA_1=BC_1,$$∠ABC=∠A_1BC_1=60°.$
$∴∠CBC_1=180°-∠ABC-∠A_1BC_1=60°.$
$∴∠C_1BA_1=∠C_1BC. $
$∵ BA_1=BC,$
$∴ BE⊥CA_1,$$CE=EA_1.$
∴点$C,$$A_1 $关于直线$BC_1$对称.
∴ 当点$D,$$B$重合时,$AD+CD$的值最小,最小值为线段$AA_1$的长,
即$AA_1=5.$
∴等边三角形$ABC$的边长为$\frac {1}{2}AA_1=\frac {5}{2}$