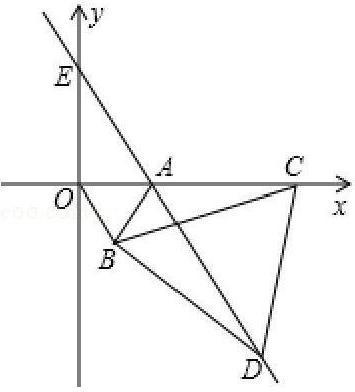
解$:(1) \triangle OBC≌\triangle ABD.$
证明:$∵\triangle AOB,$$\triangle CBD$都是等边三角形,
$∴OB=AB,$$CB=DB,$$\angle ABO= \angle DBC,$
$∴\angle OBC= \angle ABC,$
在$\triangle OBC$和$\triangle ABD$中,
$\begin{cases}OB=AB\\\angle OBC=\angle ABC\\CB=DB\ \end{cases},$
$∴\triangle OBC≌\triangle ABD(\mathrm {SAS})$
$(2)∵\triangle OBC≌\triangle ABD,$
$∴\angle BOC= \angle BAD=60^{ \circ },$
又$∵\angle OAB=60^{ \circ },$
$∴\angle OAE=180^{ \circ }-60^{ \circ }-60^{ \circ }=60^{ \circ },$
$∴\angle EAC=120^{ \circ },$$\angle OEA=30^{ \circ },$
∴以$A,$$E,$$C$为顶点的三角形是等腰三角形时,$AE$和$AC$是腰,
∵在$Rt\triangle AOE$中,$OA=1,$$\angle OEA=30^{ \circ },$
$∴AE=2,$
$∴AC=AE=2,$
$∴OC=1+2=3,$
∴当点$C$的坐标为$(3,0)$时,以$A,$$E,$$C$为顶点的三角形是等腰三角形.