电子课本网 › 第28页

第28页

信息发布者：

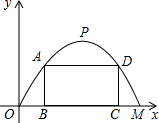
$解：(1)M(12，0)，P(6，6)$

$(2)∵顶点坐标(6，6)$

$∴设y=a(x-6)^2+6(a\neq 0)$

$又∵图象经过(0，0)$

$∴0=a(0-6)^2+6$

$∴a=-\frac {1}{6}$

$∴这条抛物线的函数解析式为y=-\frac {1}{6}(x-6)^2+6，$

$即y=-\frac {1}{6}x^2+2x.$

(3)设A(x,y)

$∴A(x，-\frac {1}{6}(x-6)^2+6)$

$∵四边形ABCD是矩形，$

$∴AB=DC=-\frac {1}{6}(x-6)^2+6，$

$根据抛物线的轴对称性，可得：OB=CM=x，$

$∴BC=12-2x，即AD=12-2x，$

$∴令L=AB+AD+DC=2[-\frac {1}{6}(x-6)^2+6]+12-2x=-\frac {1}{3}x^2+2x+12$

$=-\frac {1}{3}(x-3)^2+15.$

$∴当x=3，L最大值为15$

$∴AB、AD、DC的长度之和最大值为15米.$

$解： A(-6， 0)B(6 ， 0)C(0 ， 4)$

$方案1：设抛物线为y=ax²+4，$

$把(6，0)代入，得a=-\frac {1}{9}$

$所以y=-\frac {1}{9}x² +4$

$当y=3时，-\frac {1}{9}x²+4=3$

$解得x_{1}=-3， x_{2}=3$

$所以DE= |x_{1}- x_{2}|= 6$

$方案2 ：半径OD为6 ， $

$DE=2\sqrt{6²- 3²}=4\sqrt{3}$

$4\sqrt{3}m≈6.9m > 6m$

$所以方案2更安全$